MATH 7610

Discrete Geometry, Rigidity, and Circle Packings

Monday, Wednesday, Friday,  1:25-2:15 PM, in Malott 206

Instructor: Professor Robert Connelly

Office Hours:  MWF, 10-11:30 AM in Malott 565

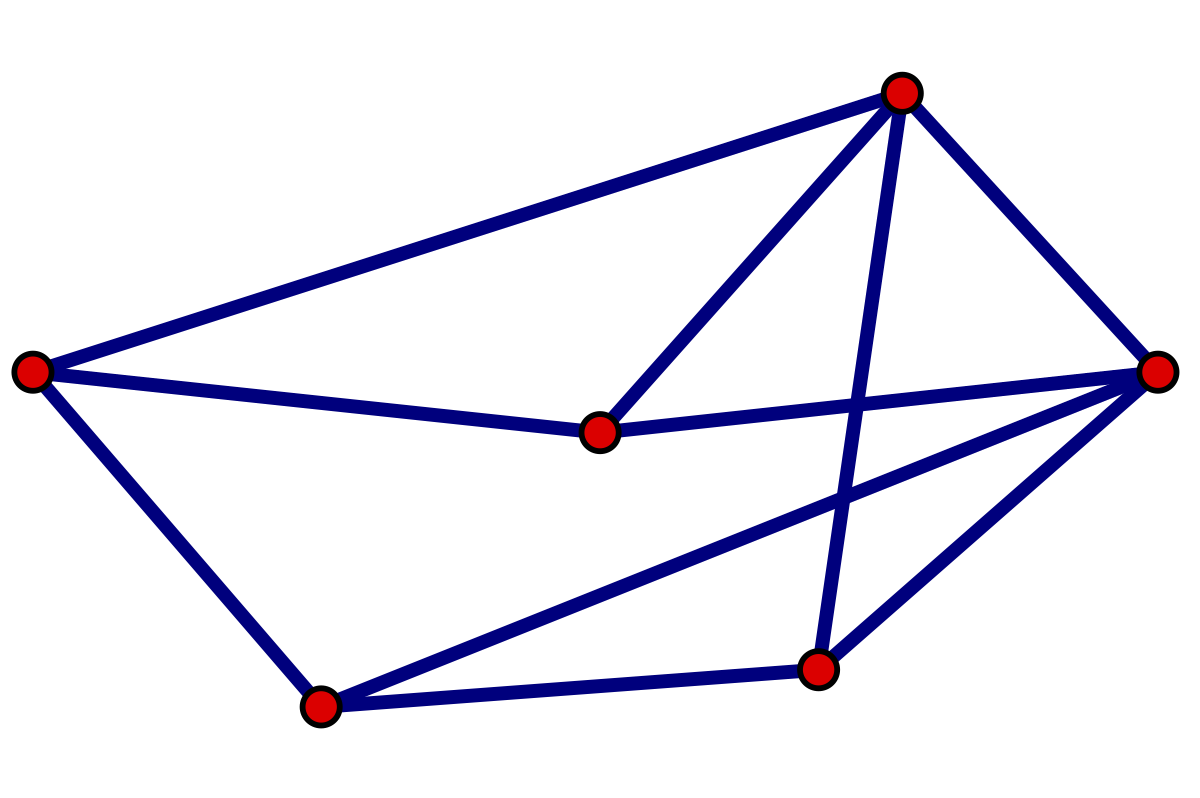
The basic object is a framework or a tensegrity framework as seen here.

The vertices are connected by rigid fixed length bars, and we fuss with what it means for it to be rigid.

Is there another configuration with the same corresponding bar lengths nearby (local rigidity), anywhere in the plane (global rigidity), or anywhere in any higher dimensional space (universal rigidity)? 

This has all kinds of connections to everyday structures as in engineering, bridges, buildings, finite mechanisms, granular materials, point location problems, packings of disks, and who knows what else.

To start we will use the book, to be published by Cambridge University Press, "Frameworks, Tensegrities and Symmetry", by Simon Guest (Chair of the Civil Engineering Department at Cambridge University) and myself as a text.  It is a gentle introduction to the subject with problems and insights, but at the end it gets into the representation theory of the finite subgroups of Euclidean space.   I will make it available to any student at Cornell.

I will invite the following people, who are active researchers in the field to come to give a talk to the class.  This will include the following:

Simon Guest at Cambridge University, England

John Bowers at the Computer Science Depart. at James Madison University

Philip Bowers at the Math Dept. at Florida State University

Steven Gortler at the Computer Science Dept. at Harvard University

Brigitte and Herman Servatius* at the Math Dept at Worcester Polytechnic Institute

Tony Nixon at the Math and Stats Dept. at Lancaster University, England

Bernd Schulze at the Math and Stats Dept. at Lancaster University, England

Miranda Holmes-Cerfon at Dept. of Math, NYU

Meera Sitharam at the Dept. of Computer and Infomation Science at the University of Florida

******Herman Servatius has agreed to come to talk to us on Sept. 18 in class.******

******Thomas Fernique has agreed to come to talk to us on the week of December (if he can get a VISA to come to the US)******

Also students in the class will be invided to lecture about parts of the book and other related subjects to be negotiated.

Here are some papers you can look at to get an idea of what we can go.

What is a tensegrity?

Universal Rigidity of a Complete Bipartite Graph

Infinitesimally Rigid Tensegrity Frameworks

Infinitesimally rigid complete bipartite frameworks, a complete story

Connection of rigidity to maximally dense packings

Introduction to global rigidity

The Isostatic Conjecture (This is an answer to the "Isostatic Conjecture" for granular materials.)

Schedule for the first few weeks:

8/30:  Introductions and basic definitions with models

9/2 to 9/9:  The Cauchy/Dehn rigidity theorem for strictly triangulated convex polytopes in 3-space.

9/11-9/13:  Generic Rigidity and Laman's Theorem, Chapter 7.

    A little puzzle:  Can you find a bar graph with n vertices on a cycle of n bars, and n-3 other bars, so that it is not generically rigid, but every pair of consequtive vertices on the cycle  have at least one other adjacent bar not part of the cycle?

Here is another puzzle:  Suppose you have a convex polygon of n cables and n vertices with n-2 bars (not necessarily struts) on the inside so that the whole framework is in generic position and isostatic, which means that it has exactly a one dimensional space of equilibrium stresses.   Is this framework  necessarily  superstable?

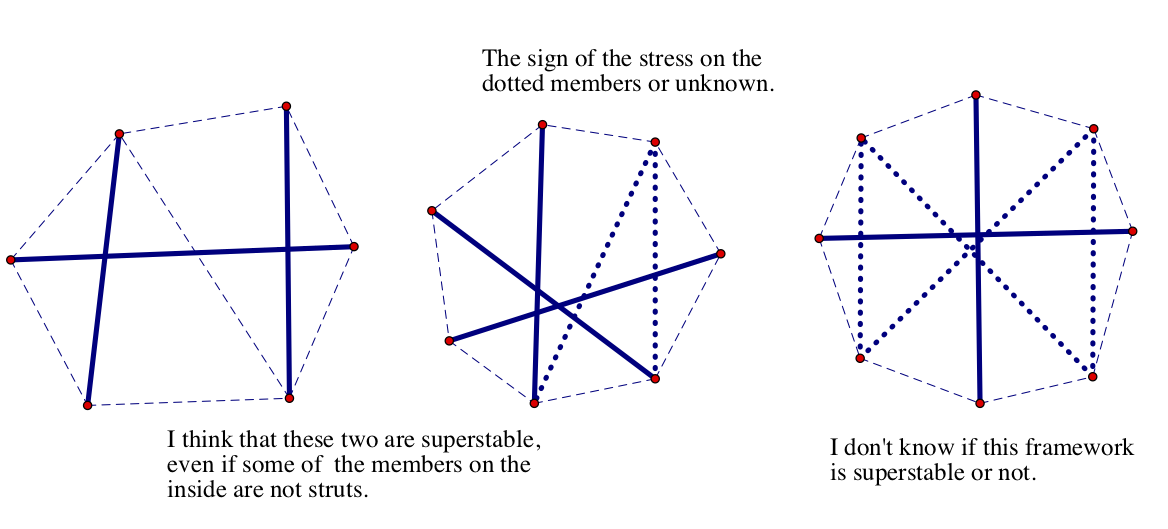
9/27:  We will a little introduction to generic global rigidity for bar frameworks.

9:30:  We will start with an introduction to circle packings and some relationships to rigidity.

9:30:  I do not know if the  middle  tensegrity has a psd equilibrium stress or not, but Zhen computes that the one on the right is not always PSD.  Sad story.  Related question:

Question:  Given a graph with a Hamiltonian cycle that generically has an equilibrium stress non-zero on all members, is there a configuration, where the Hamiltonian cycle is strictly convex with an equilibrium stress that is PSD?