Takehome Final
Due Date: Friday, December 18 (at midnight)
Rules: This is a final exam, not a homework assignment. You must solve the problems entirely on your own, and you should not discuss the problems with any other students in the class, or with anyone on the internet. Most of these problems require the use of Mathematica, and you should feel free to use Mathematica's online help system, as well as other Mathematica resources available on the web.
Note: For all questions, please make sure to fully explain the method you used to find the answer, and include any Mathematica code that was helpful. Feel free to use multiple notebooks to organize your work, but make sure to send me all of your notebooks.
- Let \(f\colon\mathbb{C}\to\mathbb{C}\) be the function \(f(z)=z^2-1\), let \(J\) be the Julia set for \(f\), and let
\(\displaystyle p \,=\, \frac{1-\sqrt{5}}{2}\) and \(\displaystyle q \,=\, \frac{-1+\sqrt{5}}{2}\).
Then \(p\) and \(q\) partition \(J\) into four pieces \(\mathsf{L}\), \(\mathsf{R}\), \(\mathsf{T}\), and \(\mathsf{B}\), as shown below.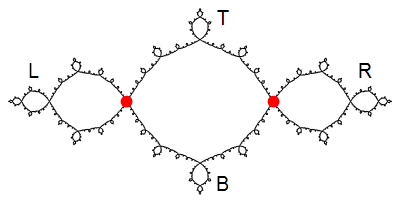 Note: The notebook
Note: The notebook FinalExamJuliaSet.nbcontains a list of 9,642 points from \(J\). This should be helpful for making pictures of the Julia set.- Use
GraphPlotto draw the transition graph for \(\mathsf{L}\), \(\mathsf{R}\), \(\mathsf{T}\), and \(\mathsf{B}\) under the map \(f\). - Draw a picture of \(J\) showing the eight level-two pieces (\(\mathsf{RR}\), \(\mathsf{RT}\), etc.). Mark each of the four breakpoints with a red dot, and use the
Textcommand to label each piece with its two-step itinerary. - Find the point on the Julia set with itinerary \(\overline{\mathsf{TLR}}\), correct to six decimal places. Draw a picture of \(J\) showing the location of this point, as well as the other two points in its orbit.
- Find the Lyapunov number of the point \(\overline{\mathsf{TLR}}\) you found in part (c), and use it to determine whether the corresponding 3-cycle is attracting or repelling.
- Use
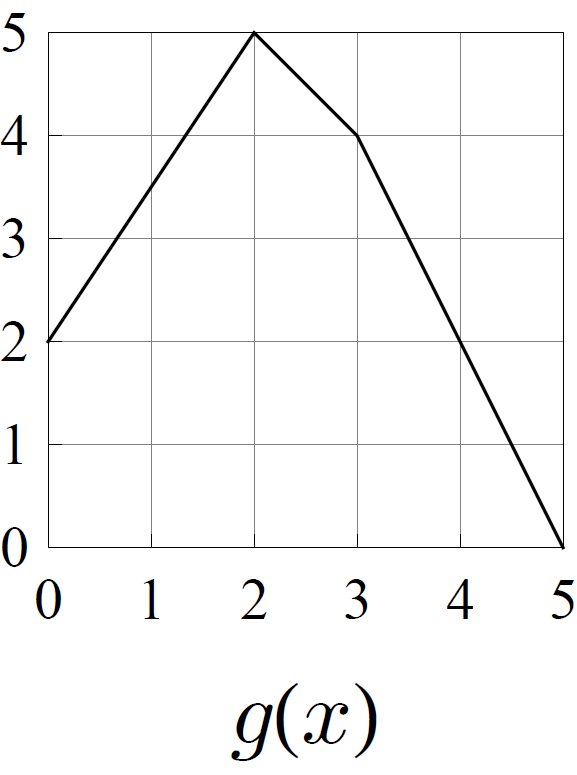
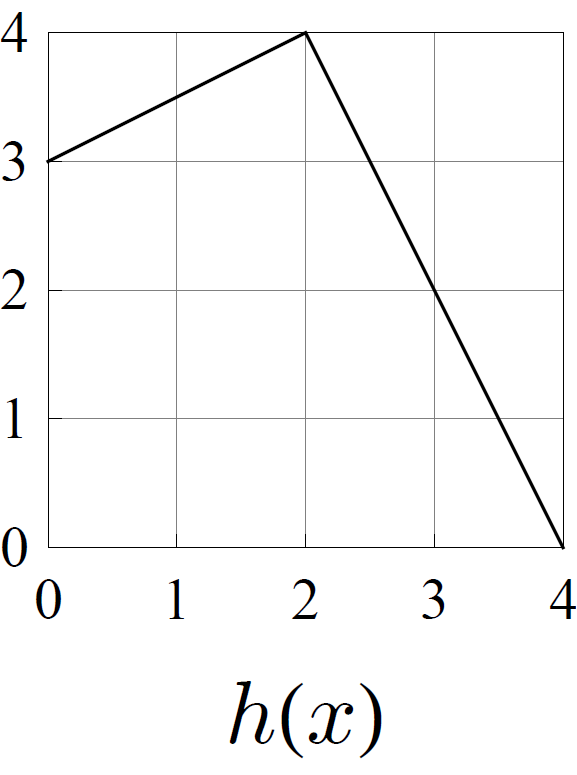
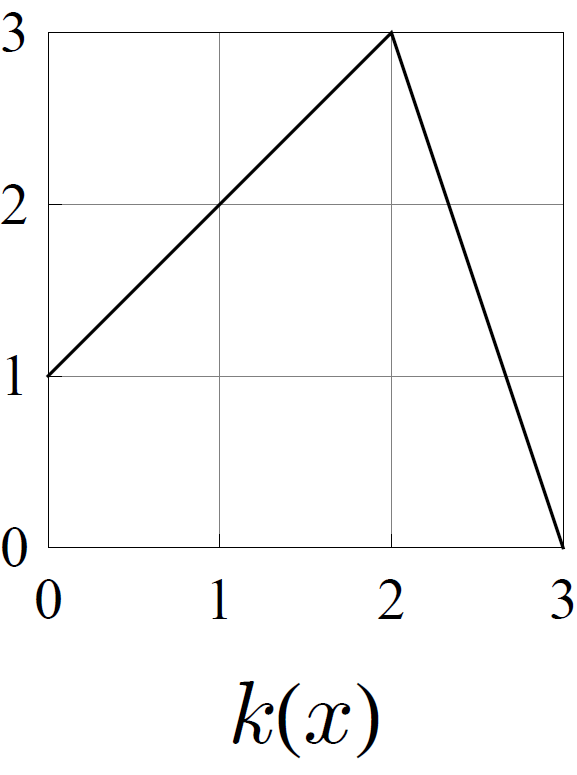
- Consider the functions \(f\), \(g\), \(h\), and \(k\) whose graphs are shown below.
Of these four functions, exactly one pair of them are topologically conjugate. Determine which two are conjugate, and find a formula for the conjugating homeomorphism.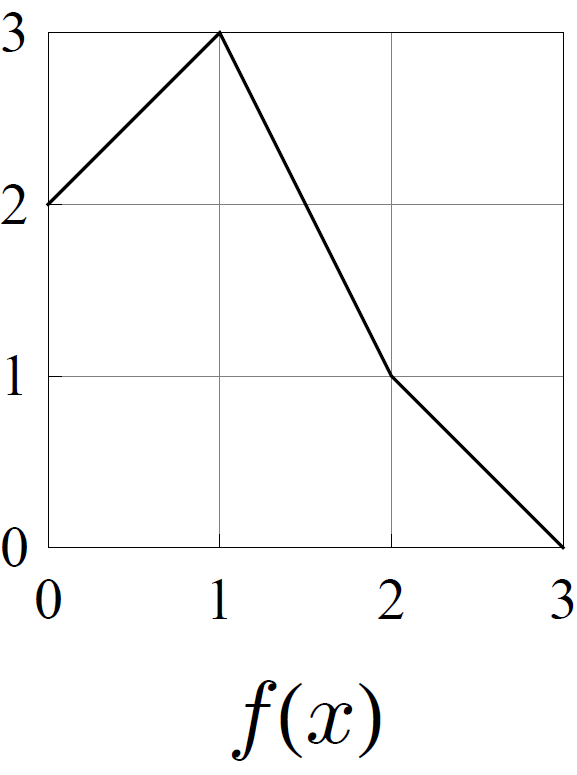
- Let \(F = \{\textbf{f}_1,\textbf{f}_2,\textbf{f}_3\}\) be the following iterated function system on the plane, whose attractor is a Sierpinski right triangle:
\(\displaystyle \textbf{f}_1(x,y) \,=\, \left(\frac{x}{2},\,\frac{y}{2}\right),\qquad\textbf{f}_2(x,y) \,=\, \left(\frac{x+1}{2},\,\frac{y}{2}\right),\qquad \displaystyle \textbf{f}_3(x,y) \,=\, \left(\frac{x}{2},\,\frac{y+1}{2}\right).\)
A cycle for \(F\) is a periodic sequence that is possible as an orbit of the iterated function system (assuming the correct random choices). For example, a 3-cycle would be a possible orbit for \(F\) of the form \[ \textbf{p}_1,\;\;\textbf{p}_2,\;\;\textbf{p}_3,\;\;\textbf{p}_1,\;\;\textbf{p}_2,\;\;\textbf{p}_3,\;\;\textbf{p}_1,\;\;\textbf{p}_2,\;\;\textbf{p}_3,\;\;\ldots \]- Find a 3-cycle for \(F\) such that \(\textbf{p}_1\) is in the top triangle, \(\textbf{p}_2\) is in the lower left triangle, and \(\textbf{p}_3\) is in the lower right triangle. Express the points as ordered pairs of fractions.
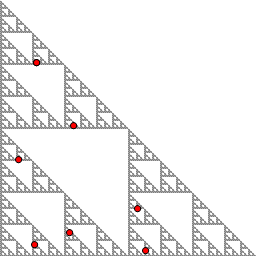
- The picture below shows the points of a certain 7-cycle for \(F\). (Click on the picture to enlarge.) Find the coordinates of the seven points of the
cycle. Express your answers as ordered pairs of fractions.