Homework 7
Due Date: Friday, November 6
- Let \(f\colon[0,1]\to[0,1]\) be the function \(f(x) = cx(1-x)\), where \(c\) is the smallest positive value for which \(1/2\) is periodic with period \(7\).
- Determine the value of \(c\). Your answer must be correct to six decimal places.
- The seven points in the orbit of \(1/2\) partition \([0,1]\) into eight intervals. Use the
Plotcommand to draw a graph of \(f\), addingGridLinesso that it is possible to see how the eight intervals map to one another. - Use
GraphPlotto draw the transition graph for \(f\) with respect to these eight intervals. Make sure that the vertex labels are shown in the graph, and include arrows along the edges to show the direction of each transition. - Find the period-\(2\) points for \(f\), correct to six decimal places. What are the itineraries of these points?
- Based on the transition graph, what is a possible itinerary for a period-\(4\) point for \(f\)?
- Based on the transition graph, does \(f\) have any points of period \(100\)? Justify your answer.
- The following picture shows a tree \(T\) in \(\mathbb{R}^2\) which is the union of four line segments \(\textsf{A}\), \(\textsf{B}\), \(\textsf{C}\), and \(\textsf{D}\):
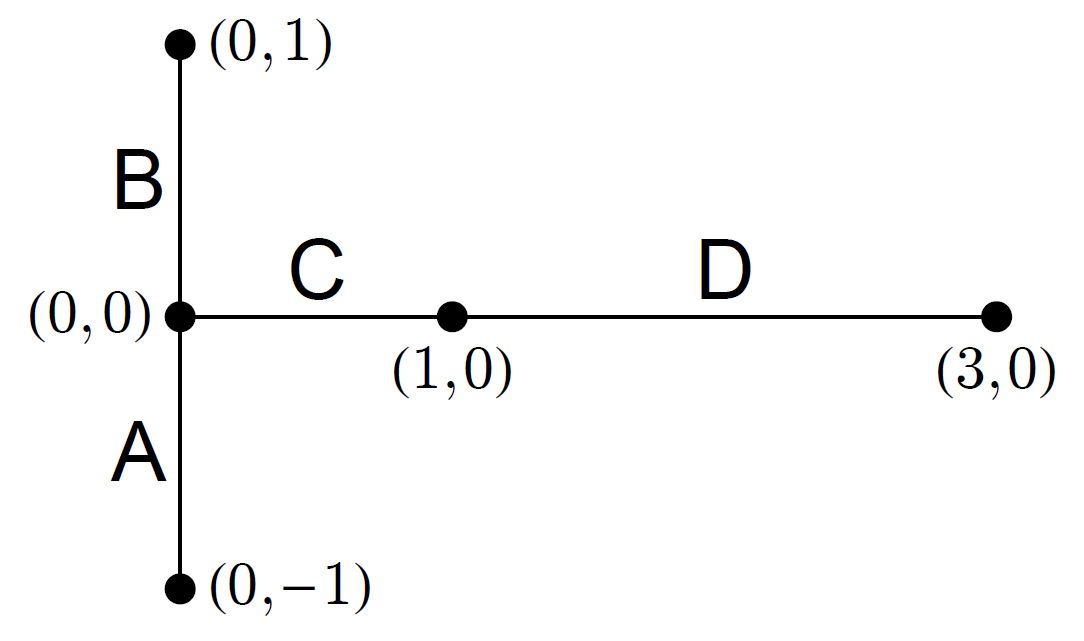 Let \(\mathbf{f}\colon T\to T\) be the continuous function with the following properties:
Let \(\mathbf{f}\colon T\to T\) be the continuous function with the following properties:
- \(\mathbf{f}(0,0) = (0,0)\), \(\mathbf{f}(0,-1) = (3,0)\), \(\mathbf{f}(1,0) = (0,1)\), \(\mathbf{f}(0,1) = \mathbf{f}(3,0) = (0,-1)\).
- \(\mathbf{f}\) maps \(\mathsf{A}\) linearly onto \(\textsf{C}\cup\textsf{D}\) (stretching by a factor of \(3\)), rotates \(\textsf{B}\) onto \(\textsf{A}\), rotates \(\textsf{C}\) onto \(\textsf{B}\), and rotates \(\textsf{D}\) onto \(\textsf{A}\cup\textsf{B}\).
- Use
GraphPlotto draw a transition graph for \(\mathbf{f}\) with respect to the line segments \(\textsf{A}\), \(\textsf{B}\), \(\textsf{C}\), and \(\textsf{D}\). - Based on the transition graph, how many period-\(5\) points does \(\mathbf{f}\) have? List the itineraries of these points.
- Find a formula for \(\mathbf{f}(x,y)\) on each of the segments \(\textsf{A}\), \(\textsf{B}\), \(\textsf{C}\), and \(\textsf{D}\).
- Find the coordinates of the period-\(3\) point with itinerary \(\overline{\textsf{DBA}}\).
- Recall that the torus \(T\) is the space of all ordered pairs \((\theta,\phi)\), where \(\theta\) and \(\phi\) are angles between \(0\) and \(2\pi\). Let \(\textsf{A}\), \(\textsf{B}\), \(\textsf{C}\), and \(\textsf{D}\) be the following four triangles on the torus:
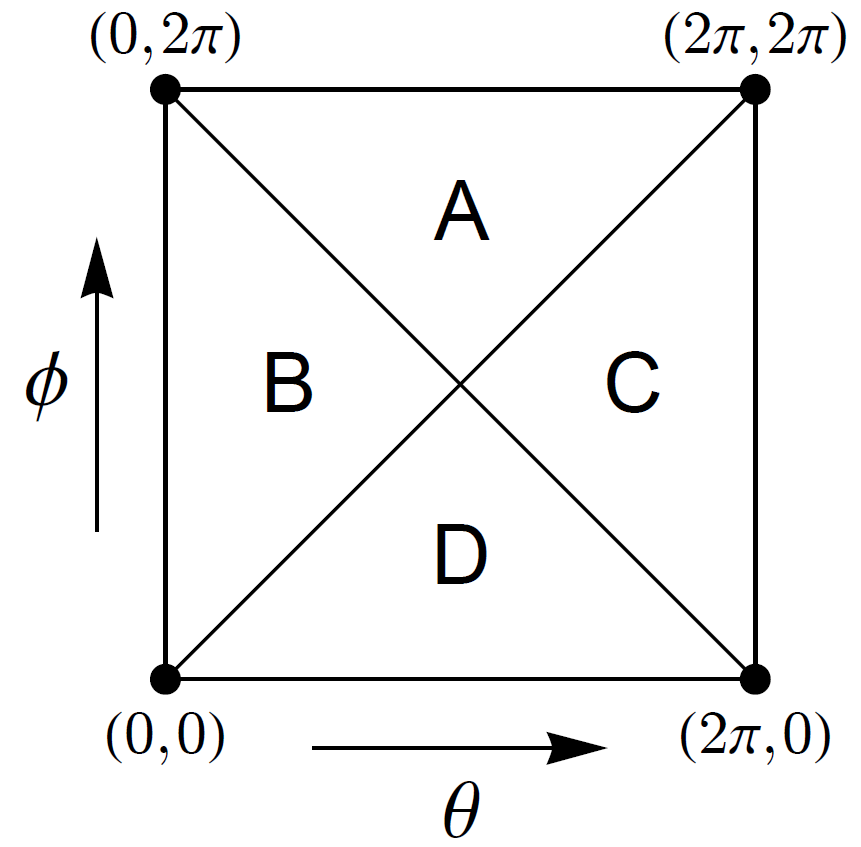 Let \(\mathbf{f}\colon T\to T\) be the function \(\mathbf{f}(\theta,\phi) = (\theta-\phi,\theta+\phi)\), where the result is interpreted as a point on the torus, e.g. \(\mathbf{f}(\pi,3\pi/2) = (-\pi/2,5\pi/2) = (3\pi/2,\pi/2)\).
Let \(\mathbf{f}\colon T\to T\) be the function \(\mathbf{f}(\theta,\phi) = (\theta-\phi,\theta+\phi)\), where the result is interpreted as a point on the torus, e.g. \(\mathbf{f}(\pi,3\pi/2) = (-\pi/2,5\pi/2) = (3\pi/2,\pi/2)\).
- Set up a
Manipulateof aListLinePlotshowing orbits of \(\mathbf{f}\) in the square. Use aLocatorto specify the initial state, and useShowto superimpose the two diagonals of the square onto the plot. Based on yourManipulate, how would you describe the dynamics of this function? - Use
GraphPlotto draw the transition graph for \(\mathbf{f}\) with respect to the four triangles \(\textsf{A},\textsf{B},\textsf{C},\textsf{D}\). - Use
Graphicsto draw a picture (similar to the one above) showing the eight triangles in the square that correspond to two-step itineraries, with each triangle labeled by the appropriate itinerary. - Based on the transition graph, how many points of period \(3\) are there for \(\mathbf{f}\,\)? List their itineraries.
- Find a formula for \(\mathbf{f}(\theta,\phi)\) on each of the triangles \(\textsf{A}\), \(\textsf{B}\), \(\textsf{C}\), and \(\textsf{D}\).
- Find the coordinates of the period-two point with itinerary \(\overline{\textsf{AD}}\). Your answer should be precise (not a decimal approximation).
- Set up a