Homework 8
Due Date: Friday, November 13
The following pictures show the first four steps in the construction of a self-similar fractal curve \(C\) in the plane:
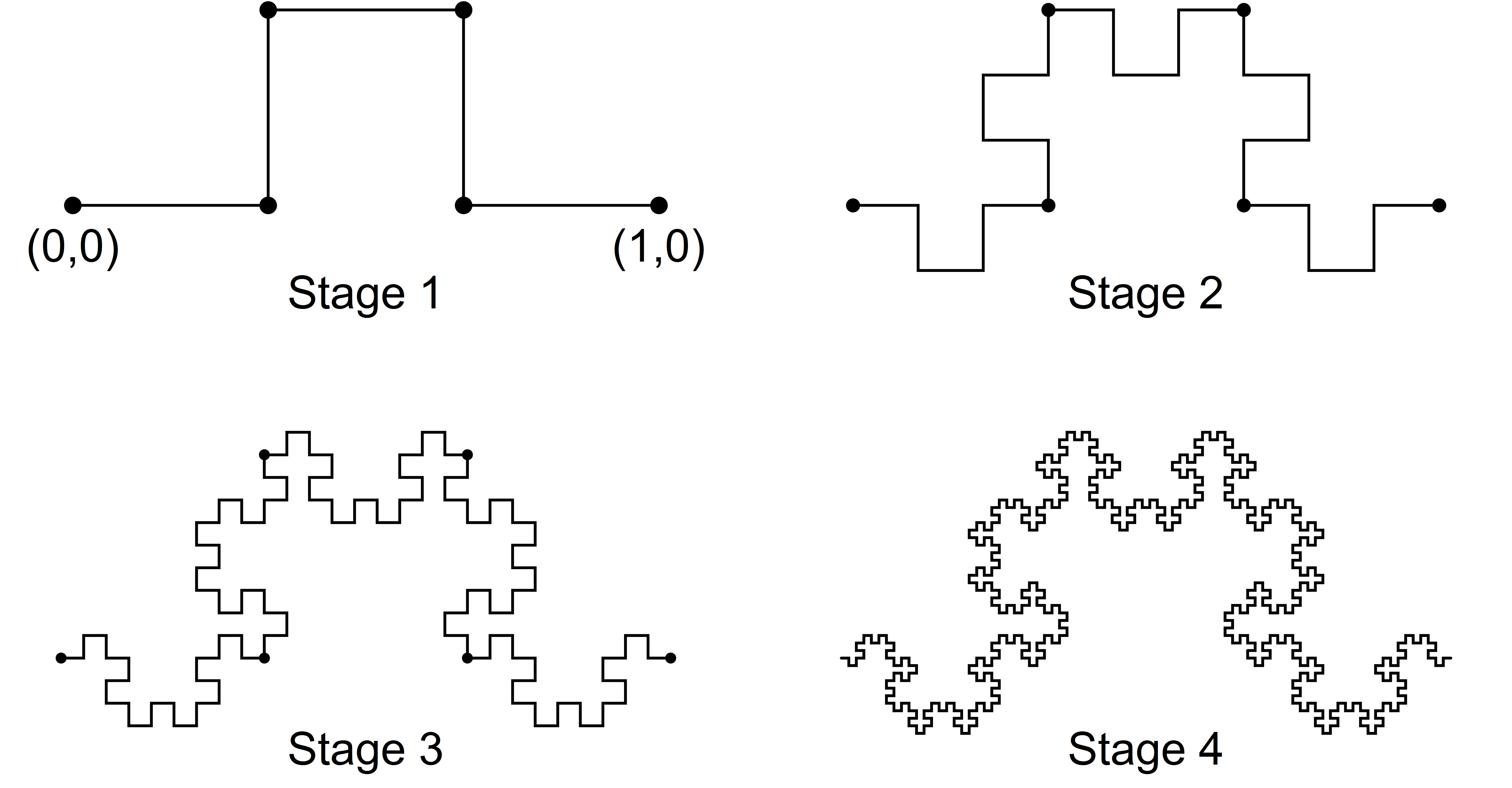 Note: The six marked points are \((0,0)\), \((1/3,0)\), \((1/3,1/3)\), \((2/3,1/3)\), \((2/3,0)\), and \((1,0)\).
Note: The six marked points are \((0,0)\), \((1/3,0)\), \((1/3,1/3)\), \((2/3,1/3)\), \((2/3,0)\), and \((1,0)\).
- Find formulas for five affine contraction maps \(\mathbf{f}_1,\mathbf{f}_2,\mathbf{f}_3,\mathbf{f}_4,\mathbf{f}_5\) that map \(C\) each of its five main pieces. Use these maps to solve the following problems.
- Create a stochastic function
iterthat implements the iterated function system consisting of the five maps \(\{\mathbf{f}_1,\mathbf{f}_2,\mathbf{f}_3,\mathbf{f}_4,\mathbf{f}_5\}\), and draw 10,000 points in a randomly determined orbit underiter. - Compute an ordered list of the corner points for each of the first six stages of the construction, and use these lists to draw pictures of each of the first six stages (similar to the pictures above).
- Create a stochastic function
-
- Find the \(y\)-coordinate of the point on \(C\) whose \(x\)-coordinate is \(1/2\). Express your answer as a fraction in lowest terms.
- Find the maximum possible \(y\)-coordinate for a point on \(C\). Express your answer as a fraction in lowest terms.