Applications of Orthogonal Polynomials on the Sierpinski Gasket
Questions
-
Can we use polynomials (orthogonal or otherwise) to accurately interpolate functions?
-
Can we obtain an analog of Gauss-Legendre quadrature on SG?
-
Can we develop an algorithm for polynomial quadrature on SG and determine error estimates for it?
Interpolation
-
Polynomials of degree \(n\) can have more than \(3n+3\) zeros on SG.
-
We need to establish the invertibility of
\[M_n = \begin{bmatrix} P_{1}(x_1) & P_{1}(x_{2}) & \dots & P_{1}(x_{3n+3})\\ \vdots & \vdots & \ddots & \vdots \\ P_{3n+3}(x_{1}) & P_{3n+3}(x_{2}) & \dots & P_{3n+3}(x_{3n+3}) \end{bmatrix}\]
If we choose a rotationally symmetric set of points, the interpolation matrix \(M_n\) becomes circulant-block. This enables us to prove the invertibility of \(M_2\).
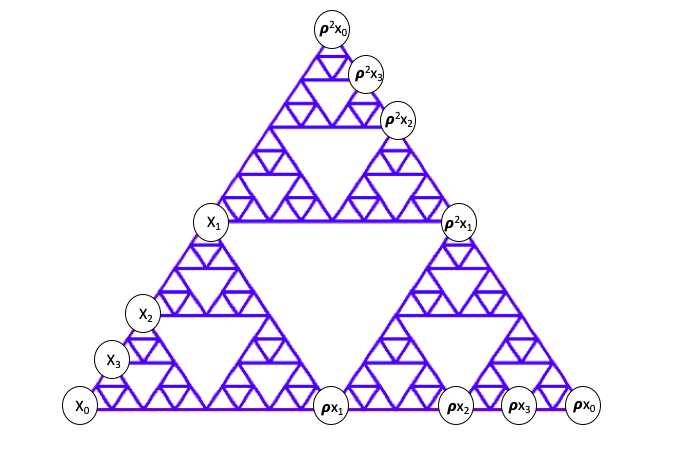
Vortex Sampling Method
| \(n\) | \(|M_n|\) |
|---|---|
| 1 | -1.744e-06 |
| 2 | 1.066e-19 |
| 3 | -4.200e-41 |
| 4 | -2.058e-69 |
| 5 | 6.788e-110 |
| 6 | -1.347e-163 |
| 7 | 5.044e-232 |
-
The interpolation matrix for the \(P_{jk}\) polynomials on \(V_1\) points is invertible (by computation)
-
By choosing \(n+1\) points on the left side of \(V_n\) along with their rotations, the interpolation matrix becomes circulant-block. These matrices are computationally invertible up to at least \(n = 50\).
-
The general case is unknown.
Note: The determinants were computed with exact rational artithmetic, so they are non-zero. The rapid decay in the determinants is due to the fact that the monomial values decay as their degree increases. As a result, solving the interpolation system computationally is not useful even though it is possible.
Quadrature
-
Gauss-Legendre quadrature on \(\mathbb{R}\) requires the polynomial division algorithm on \(\mathbb{R}\). However, we do not have this on SG.
-
We have a pseudo-division algorthim on SG, but the quotient is a linear combination of powers of the Green’s operator: \[\mathcal{Q}_f = \frac{1}{b_m} \sum\limits_{i = 0}^{n-m}c^{(i)}\mathcal{G}^{(n-m-i)}\]
-
We can try to use n-Harmonic spline quadrature, but this comes back to the interpolation problem since we need to solve \[\begin{bmatrix} P_{1}(x_1) & P_{1}(x_{2}) & \dots & P_{1}(x_{3n+3})\\ \vdots & \vdots & \ddots & \vdots \\ P_{3n+3}(x_{1}) & P_{3n+3}(x_{2}) & \dots & P_{3n+3}(x_{3n+3}) \end{bmatrix} \begin{bmatrix} w_1\\ \vdots\\ w_{3n+3} \end{bmatrix} = \begin{bmatrix} \int_{SG}P_{01}\\ \vdots\\ \int_{SG}P_{n3} \end{bmatrix}\]
N-Harmonic Extension: The Solution to Many Polynomial Problems on SG
-
Is there an algorithm to extend a function defined on \(3n+3\) vertices of \(V_n\) n-Harmonically?
-
Given this algorithm, we have the following quadrature error estimate: \[\left|I_n^m(f) - \int_{SG}f\right|\leq c_15^{-(n+1)(m-n)}\|\Delta^{(n+1)}f\|_\infty\]
Outstanding Questions Regarding Polynomials on SG
-
Is \(\partial_nf_n \neq 0 \ \forall \ n\)?
-
Is \(P_{j1} > 0\) except at \(q_0\)?
-
Interpolation problem: Does sampling an \(n\) degree polynomial on any \(3n + 3\) points uniquely determine the polynomial?
Questions 2 and 3 can be solved given an n-Harmonic Extension Algorithm.