Chebyshev Polynomials on the Sierpinski Gasket
Extrema of Polynomials
Definition of local extrema:
-
For a function \(u\) defined on SG and \(x\in SG\), we say that \(x\) is a local maximum (minimum) of \(u\) if \(\exists\) neighborhood \(U\) s.t. \(x\in U\subseteq SG\) and \(\forall y\in U\), we have \(u(x)\geq u(y)\) (or \(u(x)\leq u(y)\)).
-
For a function \(u\) defined on SG and \(x=F_{w}q_{n}=F_{w'}q_{n'}\in SG\), we say that \(x\) is a local edge maximum (minimum) of \(u\) if \(\exists\) \(M\) s.t. \(\forall m\geq M\), \(u(x)\geq u(F_{w}F_{n}^{m}q_{j})\) for \(j=n-1,n+1\) and \(u(x)\geq u(F_{w'}F_{n'}^{m}q_{j'})\) for \(j'=n'-1, n'+1\). [\(u\) is larger than a discrete set of points on all neighboring edges]
\(\Rightarrow\) Local edge extrema are weaker than local extrema.
General Case
Theorem:
(Necessary conditions for \(x\) to be a local edge extrema of \(u\))
-
If \(x\in V_{0}\) is on the boundary, then \(\partial_{n}u(x)\geq 0\) if \(x\) is a local maximum (or \(\partial_{n}u(x)\leq 0\) for \(x\) a local minimum)
-
If \(x\) is not on the boundary, then \(\partial_{n}u(x)=0\), and \(\Delta u(x)\leq 0\) if \(x\) is a local maximum (or \(\Delta u(x)\geq 0\) if \(x\) is a local maximum)
Corollary: \(P_{11}\geq 0\)
Theorem:
(Sufficient conditions for \(x\) to be a local edge extrema of \(u\))
-
Let \(u\in dom\Delta_{\mu}\) and \(x=F_{w}q_{n}=F_{w'}q_{n'}\) be a junction point satisfying \(\begin{cases} \Delta u(x)<0 \text{ (or } \Delta u(x)>0) \\ \partial_{n}u(F_{w}q_{n})=\partial_{n}u(F_{w'}q_{n'})=0 \\ \partial_{T}u(F_{w}q_{n})=\partial_{T}u(F_{w'}q_{n'})=0 \end{cases}\)
Then \(t\) is a local edge maximum (or minimum) of \(u\) on SG.
\(\Rightarrow\) This only holds for local edge maximum, not local maximum. (Normal derivatives and tangential derivatives are very weak characterizations of local behavior)
Harmonic Case
Lemma: (Behavior of Harmonic Function on Outmost Edges)
Let \(h\) be a harmonic function on SG, and we consider the edge between \(q_{0}, q_{1}\in V_{0}\), assuming \(h(q_{0})\leq h(q_{1})\).
-
If \(\partial_{n}h(q_{0})\cdot \partial_{n}h(q_{1})\leq 0\), then \(h\) is increasing from \(q_{0}\) to \(q_{1}\).
-
If \(\partial_{n}h(q_{0}), \partial_{n}h(q_{1})>0\), then \(h\) first decrease then increase from \(q_{0}\) to \(q_{1}\).
-
If \(\partial_{n}h(q_{0}), \partial_{n}h(q_{1})<0\), then \(h\) first increase then decrease from \(q_{0}\) to \(q_{1}\).
\(\Rightarrow\) Behavior of harmonic functions on edges is completely characterized by sign of normal derivatives on \(V_{0}\).
\(\Rightarrow\) This only holds for local edge maximum, not local maximum. (Normal derivatives and tangential derivatives are very weak characterizations of local behavior)
Theorem: (Local Extrema of Harmonic Functions)
Let \(h\) be a non-constant harmonic function: \(h(q_{0})=\alpha\), \(h(q_{1})=\beta\), \(h(q_{2})=\gamma\) with \(\alpha\leq \beta\leq \gamma\) not all equal.
-
If \(\partial_{n}h(q_{1})=0\), then \(q_{0}\) is the unique local minimum and \(q_{2}\) is the unique local maximum.
-
If \(\partial_{n}h(q_{1})<0\), then \(q_{0}\), \(q_{1}\) are the only local minima and \(q_{2}\) is the unique local maximum.
-
If \(\partial_{n}h(q_{1})>0\), then \(q_{0}\) is the unique local minimum and \(q_{1}, q_{2}\) are the only local maxima.
Biharmonic Case
Theorem:
(Necessary conditions for local extrema of biharmonic functions)
Let \(u\in\mathcal{H}^{1}\) be a nonconstant biharmonic function on SG, and \(x=F_{w}q_{n}=F_{w'}q_{n'}\) be a junction point that is a local extrema of \(u\). Then we have:
-
\(\partial_{n}u(x)=0\).
-
Either \(\Delta u(x)\neq 0\) or \(\partial_{n}\Delta u(x)\neq 0\).
\(\Rightarrow\) Proof: From the properties of antisymmetric functions.
Theorem:
(Sufficient conditions for local extrema of biharmonic functions)
Let \(u\in\mathcal{H}^{1}\) be a function on \(SG\), and \(x=F_{w}q_{n}=F_{w'}q_{n'}\) be a junction point. Suppose \(\begin{cases} \partial_{n}u(x) = 0 \\ \partial_{T}u(x) = 0 \\ \partial_{n}\Delta u(x) = 0 \\ \partial_{T}\Delta u(x) = 0 \end{cases}\), then \(x\) is a local optimum of \(u\).
\(\Rightarrow\) This comes from the property that \(P_{11}\) achieves global maximum/minimum on the boundary.
Recap
-
Define local extrema and local edge extrema
-
Local edge extrema + functions in the domain of Laplacian
-
Local extrema + harmonic/biharmonic functions
Questions to Consider
-
Can any of the above be generalized to n-harmonic functions?
-
Is it possible to design an efficient algorithm to find local extrema of n-harmonic functions, given that we can evaluate the \(n\)-jet at all points?
Chebyshev Polynomials on SG
Definition of Chebyshev Polynomials on \([-1,1]\): The \(n^{th}\) Chebyshev polynomial \(T_{n}(x): [-1, 1] \rightarrow \mathbb{R}\) is defined as \(T_{n}(x) := \cos(n\cos^{-1}(x))\) An important property of Chebyshev Polynomials on \([-1,1]\) is the extremal principle: \(\forall P(x):[-1,1] \rightarrow \mathbb{R}\), monic polynomial of degree \(n\), \(||2^{1-n}T_{n}(x)||_{u} \leq ||P(x)||_{u}\), where \(|| \cdotp ||_{u}\) is the uniform norm of functions. Remark: the leading coefficient of \(T_{n}(x)\) is \(2^{1-n}\), and hence \(2^{1-n}T_{n}(x)\) is the monic polynomial on \([-1,1]\) that minimizes the uniform norm.
The revised definition of Chebyshev Polynomials on any compact \(K \subseteq \mathbb{R}\): The \(n^{th}\) Chebyshev polynomial \(T_{n}(x): K \rightarrow \mathbb{R}\) is defined as the monic polynomial of degree \(n\) that has the smallest uniform norm of all monic polynomial of degree \(n\). Fix \(k\), then the monic polynomial of degree \(j\) is a polynomial of the form \(\sum_{l=0}^{j}c_{l}P_{lk}\), where \(c_{j} = 1\). Definition of the \(j^{th}\) Chebyshev Polynomials of family \(k\) on SG: Fix \(k = 1,2,3\), then the \(j^{th}\) Chebyshev Polynomials of family \(k\), \(T_{jk}(x)\), is the monic polynomial of degree \(j\), such that \(\forall P(x)\) a monic polynomial of degree \(j\), \(||T_{jk}||_{u} \leq ||P||_{u}\)
The problem right now reduces to for fixed \(k\), find \(a_{k}\), such that \(P_{1k}(x)+a_{k}P_{0k}(x)\) has the smallest uniform norm of all monic polynomial of degree \(1\).
-
For the 1-family, we have an exact answer, that \(T_{11}(x) = P_{11}(x)-\frac{1}{12}P_{01}(x)\)
-
This is because \(P_{11} \geq 0\) and hence it achieves the minimum value \(0\) at \(q_{0}\) and the maximum value \(\frac{1}{6}\) at \(q_{1}\) and \(q_{2}\).
-
Unfortunately, the proof that \(P_{11} \geq 0\) is overcomplicated and cannot be generalized to arbitrary \(j\).
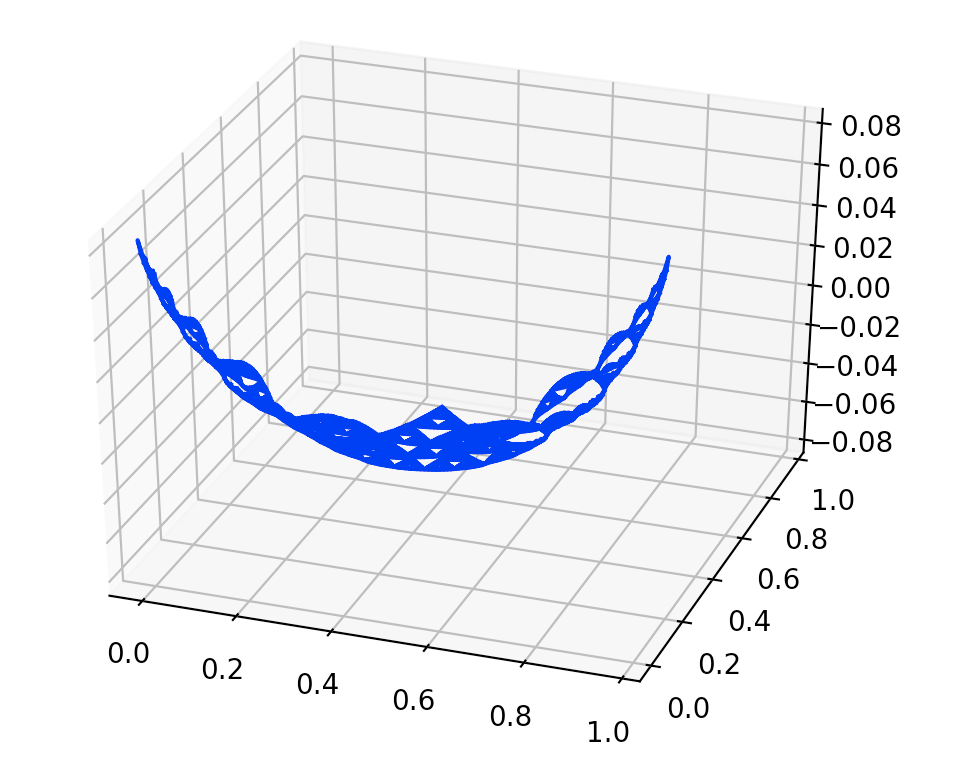
Plot of Chebyshev polynomial of order \(1\) of family \(1\), with \(a=-\frac{1}{12}\). The boundary node on the left is \(q_{1}\), the one on the right is \(q_{2}\), and the boundary node on the back is \(q_{0}\).
Partial Results on \(\mathcal{H}_1\)
-
For the \(2^{nd}\) Chebyshev polynomials of family \(2\) and the family \(3\), we only have experimental result, and our experiments show that \(a_{2} = −0.0619339\) and \(a_{3} = −0.0275013\)
-
We found those values by firstly determining loose bounds of \(a_{2}\) and \(a_{3}\), which are \([-\frac{2\beta_{1}}{\beta_{0}}, 0]=[-\frac{8}{45}, 0]\) for \(a_{2}\) and \([-\frac{2\alpha_{1}}{\alpha_{0}}, 0]=[-\frac{1}{15}, 0]\) for \(a_{3}\).
-
Then we partition the intervals, test out each \(a_{k}\), and look for the \(a_{k}\) that gives the smallest uniform norm.
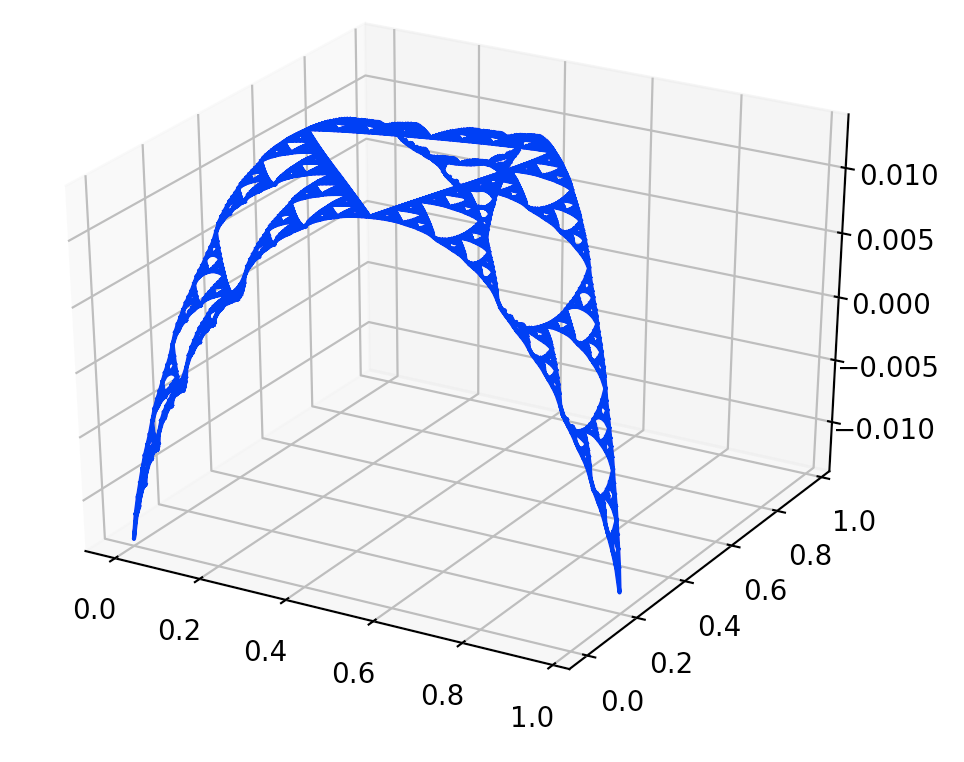
Plot of Chebyshev polynomial of order \(1\) of family \(2\), with \(a\approx -0.0619339\). The boundary node on the left is \(q_{1}\), the one on the right is \(q_{2}\), and the hidden boundary node on the back is \(q_{0}\).
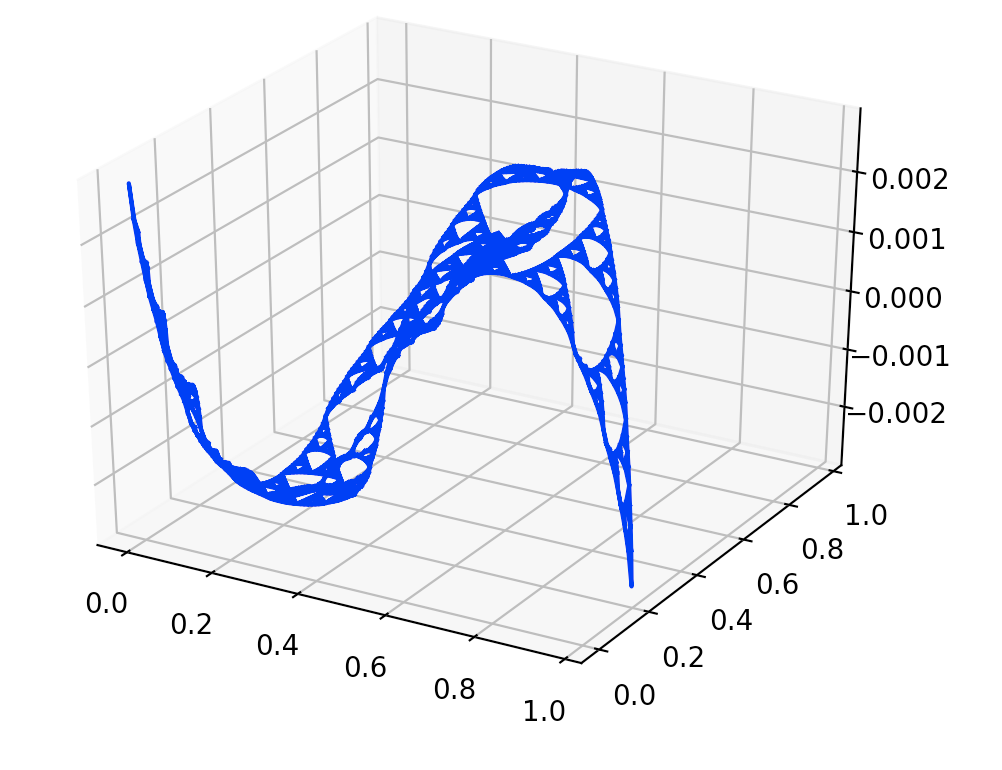
Plot of Chebyshev polynomial of order \(1\) of family \(3\), with \(a\approx -0.02750235\). The boundary node on the left is \(q_{1}\), the one on the right is \(q_{2}\), and the hidden boundary node on the back is \(q_{0}\).
Alternating Property of Chebyshev Polynomials
-
A degree \(n\) polynomial \(P_{n}(x)\) defined on a compact set \(K \subseteq \mathbb{R}\), has an alternating set, if \(\exists \{x_{j}\}_{j=0}^n\) with \(x_{0} < x_{1} < ...< x_{n}\), so that \(P_{n}(x_{j}) = (-1)^{n-j}||P_{n}(x)||_{u}\).
-
The Alternation Theorem: A monic polynomial of degree n is the Chebyshev polynomial if and only if it has an alternating set.
-
The experimental results also show that the absolute value of the minimum and the maximum of the monic polynomials become closer when \(a_{2}\) and \(a_{3}\) approach the values that minimize their uniform norms.
-
Assume that there exist an \(a\), such that \(Q(x) := P_{13}(x)+aP_{03}(x)\) achieves maximum norm at two distinct points \(y \in \bigcup\limits_{m=0}^{\infty} F_{0}^{m}F_{1}SG\) and \(z \in \bigcup\limits_{m=0}^{\infty} F_{0}^{m}F_{1}SG\), and \(z = -y\). Then \(Q(x)\) is the \(1^{st}\) Chebyshev polynomial of the 3-family.
-
Assume \(Q(x)\) is not the first Chebyshev polynomial of the 3-family. Then \(||T_{13}||_{\infty} < ||Q||_{\infty}\). This implies that \(|T_{13}(x)| < |Q(x)|\) at \(y\) and \(z\). Thus \(T_{13} - Q(x)\) cannot be both positive or negative at \(y\) and \(z\). Since both \(T_{13}(x)\) and \(Q(x)\) are monic, \(T_{13} - Q(x)\) is spanned by \(P_{03}\), and hence \(T_{13} - Q(x)\) has to be both positive or negative at \(y\) and \(z\). We have a contradiction.
Further Questions
-
Find explicit formulas for Chebyshev polynomials of any degree.
-
Replicate the alternation theorem to polynomials on SG.
-
Study the orthogonality.
-
Find the recurrence relation, if any.