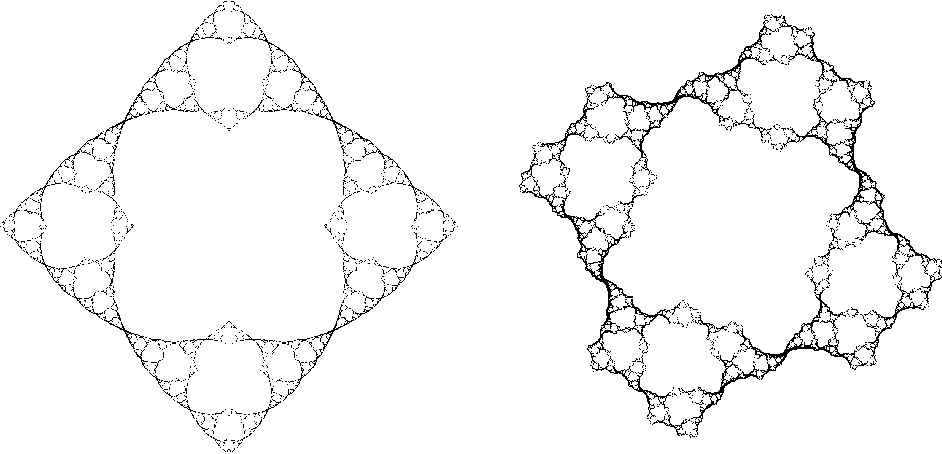
The theory provides a large class of Julia sets with a generalized Sierpinski Gasket appearance.
The theory of Julia sets can be generalized to rational functions which are quotients of complex valued polynomials. Focussing on special cases of Misiurewicz rational maps one has found Julia sets which look like generalized Sierpinski gaskets. The combinatorical properties of these fractals are connected to a deep theory in Complex Dynamics. This approach has been applied especially for the Julia set which is homeomorphic to the well-known Sierpinski gasket. Firstly, one has a connection from SG as a "man-made" fractal defined via three linear maps to a naturally ocurring fractal defined via a rational map living on the Riemann sphere. This theory gives rise to a new Iterated Function System and a new space of energy forms.
Have a look at the paper.

The theory provides a large class of Julia
sets with a generalized Sierpinski Gasket appearance.
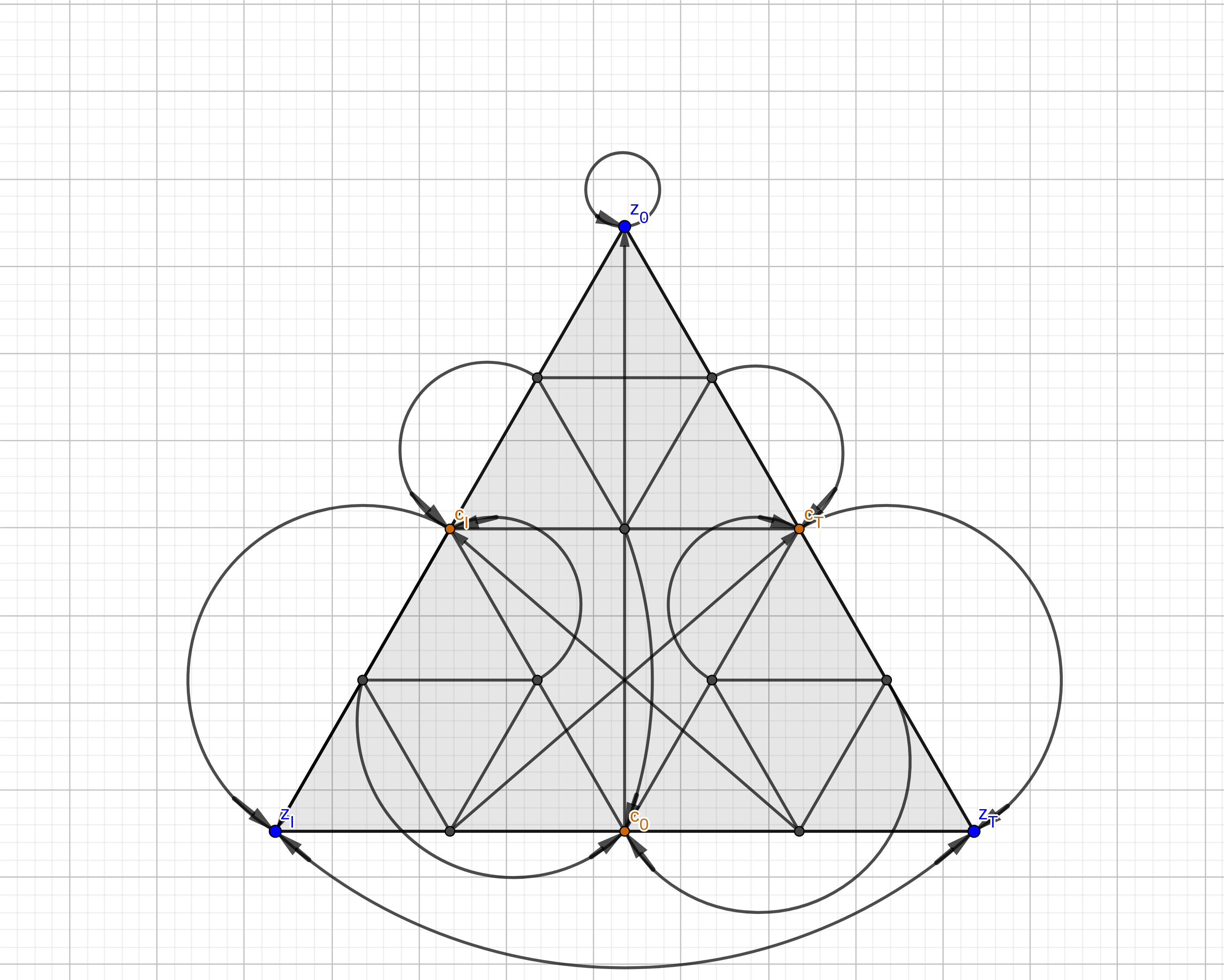
The rational map on the second step
of the graph approximation on SG.